Assignment 4: divisible by three – Embarking on Assignment 4: Divisibility by Three, we delve into the fascinating realm of mathematics, exploring the intriguing concept of divisibility by three. This fundamental principle underpins numerous applications in various disciplines, making it an essential topic for exploration.
Throughout this assignment, we will unravel the mathematical underpinnings of divisibility by three, examining its properties, characteristics, and practical applications. By delving into various methods for testing divisibility and exploring its significance in number theory, we will gain a comprehensive understanding of this important mathematical concept.
Divisibility by Three

Divisibility by three is a fundamental mathematical concept that determines whether a given integer can be evenly divided by the number three. Understanding this concept is essential in various branches of mathematics, including number theory, algebra, and calculus.
Properties and Characteristics
Numbers that are divisible by three possess certain properties and characteristics that distinguish them from other integers. These properties include:
- Sum of Digits:The sum of the individual digits of a number that is divisible by three is also divisible by three. For example, the number 123 is divisible by three because 1 + 2 + 3 = 6, which is also divisible by three.
- Remainder of 0:When a number is divided by three, the remainder is either 0, 1, or 2. If the remainder is 0, the number is divisible by three.
- Alternating Pattern:The digits of a number that is divisible by three alternate between odd and even, starting with an odd digit. For example, the number 123456 is divisible by three because the digits alternate between odd (1, 3, 5) and even (2, 4, 6).
Testing Divisibility by Three

Determining whether a number is divisible by three is a fundamental arithmetic operation. There are several methods for testing divisibility by three, each with its advantages and applications.
Sum of Digits Method
The sum of digits method involves adding up the individual digits of a number. If the sum is divisible by three, then the original number is also divisible by three.
Example:
- Consider the number 123. The sum of its digits is 1 + 2 + 3 = 6, which is divisible by three. Therefore, 123 is divisible by three.
- For the number 456, the sum of digits is 4 + 5 + 6 = 15, which is not divisible by three. Thus, 456 is not divisible by three.
Remainder on Division by 3 Method
The remainder on division by 3 method involves dividing the number by three and examining the remainder. If the remainder is zero, then the number is divisible by three.
Example:
- Dividing 123 by 3 results in a quotient of 41 and a remainder of 0. Since the remainder is zero, 123 is divisible by three.
- When 456 is divided by 3, the quotient is 152 and the remainder is 0. Again, the remainder is zero, indicating that 456 is divisible by three.
The remainder on division by 3 method is particularly useful when dealing with large numbers, as it does not require the calculation of the sum of digits.
Applications of Divisibility by Three: Assignment 4: Divisible By Three
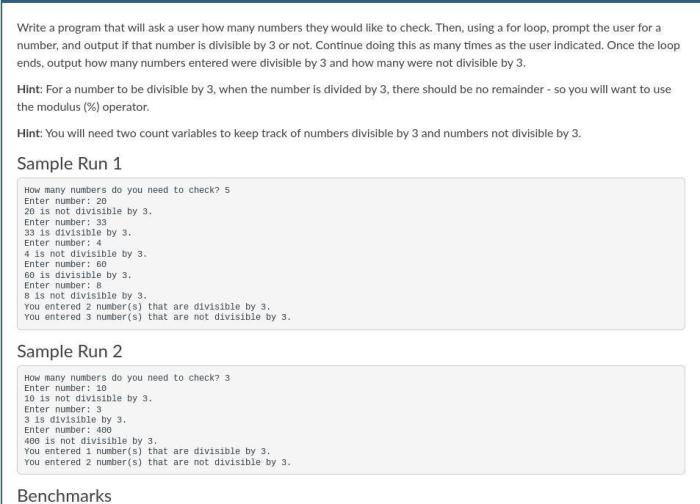
Divisibility by three has numerous practical applications in various fields, including problem-solving, decision-making, and specific disciplines like mathematics, computer science, and finance.
Problem-Solving and Decision-Making
Divisibility by three can simplify problem-solving and decision-making processes. For example, when distributing items equally among a group of people, checking if the total number of items is divisible by the number of people ensures an equal distribution without any leftovers.
Mathematics
In mathematics, divisibility by three plays a crucial role in number theory and modular arithmetic. It helps determine the divisibility of sums, differences, and products of integers. Furthermore, it aids in solving linear equations and understanding the properties of prime numbers.
Computer Science
In computer science, divisibility by three is used in algorithms and data structures. For instance, in hashing techniques, the size of a hash table is often chosen to be a prime number that is not divisible by three, as it minimizes collisions and improves performance.
Finance
In finance, divisibility by three is utilized in calculating interest payments, determining loan terms, and assessing financial ratios. For example, if an interest rate is 6%, the total interest paid over a three-year period will be divisible by three.
Number Theory and Divisibility
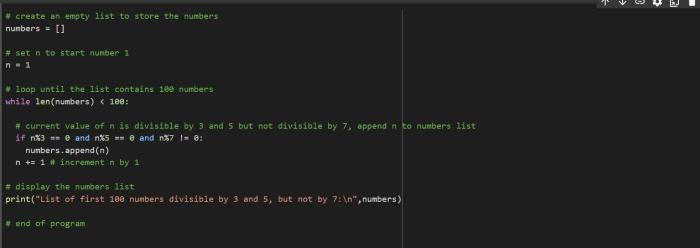
Number theory, a branch of mathematics that delves into the properties of positive integers, has a profound connection with divisibility by three. Divisibility by three plays a crucial role in understanding the structure of numbers, their factorization, and their relationships.
Prime Factorization and Divisibility by Three
Prime factorization is the process of expressing a number as a product of its prime factors, which are numbers greater than 1 that are divisible only by themselves and 1. Divisibility by three provides a valuable tool in prime factorization.
A number is divisible by three if and only if the sum of its digits is divisible by three. This property can be used to quickly identify numbers that have 3 as a prime factor.
Greatest Common Divisors and Divisibility by Three
The greatest common divisor (GCD) of two or more numbers is the largest number that divides all of the given numbers without leaving a remainder. Divisibility by three can simplify the process of finding the GCD. If two numbers are both divisible by three, then their GCD is also divisible by three.
This property can be used to reduce the number of calculations required to find the GCD.
Applications in Mathematical Theorems, Assignment 4: divisible by three
Divisibility by three has numerous applications in proving mathematical theorems. For example, Fermat’s Little Theorem states that for any prime number pand any integer a, ap– ais divisible by p. This theorem can be proven using divisibility by three. Additionally, divisibility by three is used in the proof of Wilson’s Theorem, which states that for any prime number p, ( p– 1)! + 1 is divisible by p.
FAQ Compilation
What is divisibility by three?
Divisibility by three refers to the mathematical property of a number being divisible by three without leaving a remainder.
How can we test if a number is divisible by three?
There are several methods for testing divisibility by three, including the “sum of digits” method and the “remainder on division by 3” method.
What are the practical applications of divisibility by three?
Divisibility by three finds applications in various fields, such as problem-solving, decision-making, and fields like mathematics, computer science, and finance.