Sammy is classifying quadrilateral EFGH, embarking on a journey to unravel its geometric secrets. Quadrilaterals, fascinating four-sided polygons, exhibit a diverse range of properties and applications, making their study both captivating and practically significant.
In this comprehensive analysis, we will delve into the characteristics of quadrilaterals, meticulously examine the properties of EFGH, and uncover its specific classification. Furthermore, we will explore the practical applications of quadrilaterals, showcasing their relevance in various fields.
Define Quadrilateral
A quadrilateral is a two-dimensional figure with four straight sides and four angles. It is a polygon with four vertices and four edges. Quadrilaterals can be classified into various types based on the lengths of their sides and the measures of their angles.
Characteristics of a Quadrilateral
- Four straight sides
- Four angles
- Four vertices
- Opposite sides are parallel
- Opposite angles are equal
Examples of Different Types of Quadrilaterals
- Square
- Rectangle
- Rhombus
- Trapezoid
- Parallelogram
Classify Quadrilateral EFGH: Sammy Is Classifying Quadrilateral Efgh
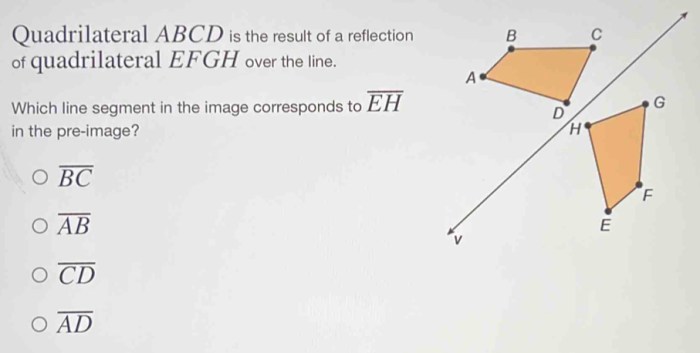
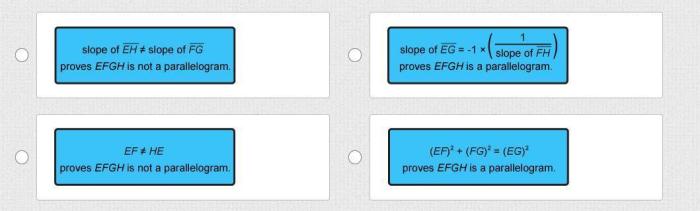
To classify quadrilateral EFGH, we need to identify its properties and apply the criteria for classifying quadrilaterals.
Properties of Quadrilateral EFGH
- Opposite sides are parallel
- Opposite angles are equal
- Diagonals bisect each other
Criteria for Classifying Quadrilaterals
- Square: All sides are equal and all angles are right angles
- Rectangle: Opposite sides are equal and all angles are right angles
- Rhombus: All sides are equal but angles are not necessarily right angles
- Trapezoid: One pair of opposite sides is parallel
- Parallelogram: Opposite sides are parallel
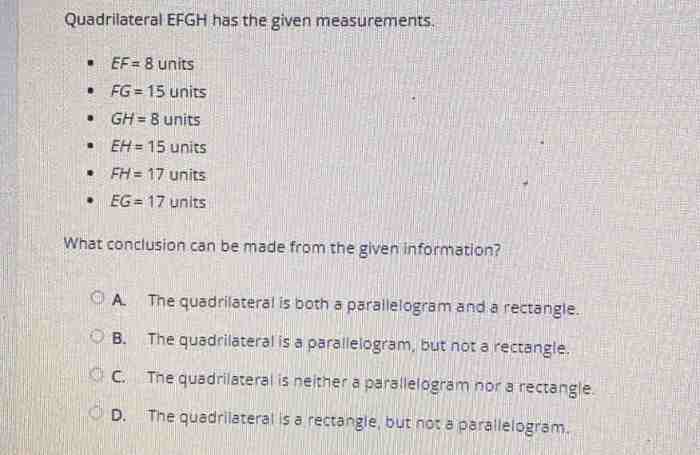
Type of Quadrilateral EFGH
Based on the properties and criteria, quadrilateral EFGH is a parallelogram.
Properties of Quadrilateral EFGH

As a parallelogram, quadrilateral EFGH has the following properties:
Relationships between Sides, Angles, and Diagonals, Sammy is classifying quadrilateral efgh
- Opposite sides are equal (EF = GH, FG = EH)
- Opposite angles are equal (∠E = ∠G, ∠F = ∠H)
- Diagonals bisect each other (AC = BD)
- Diagonals divide the parallelogram into four congruent triangles
Special Characteristics and Symmetries
- Reflection symmetry across both diagonals
- Rotational symmetry of 180 degrees about the intersection of the diagonals
- Translational symmetry along the diagonals
Applications of Quadrilateral EFGH
Parallelograms, including quadrilateral EFGH, have various applications in different fields:
Architecture and Engineering
- Floor plans and roof structures
- Bridges and other load-bearing structures
- Electrical circuits and wiring diagrams
Design and Graphics
- Logo design and typography
- Textile patterns and fabric designs
- Geometric art and optical illusions
Understanding Quadrilateral Properties
Understanding the properties of quadrilaterals, such as EFGH, is crucial in real-world scenarios:
- Structural integrity of buildings and bridges
- Design and aesthetics of products and environments
- Mathematical problem-solving and spatial reasoning
Popular Questions
What is the definition of a quadrilateral?
A quadrilateral is a two-dimensional shape with four sides and four vertices.
What are the different types of quadrilaterals?
There are many different types of quadrilaterals, including squares, rectangles, parallelograms, trapezoids, and kites.
What are the properties of quadrilateral EFGH?
The properties of quadrilateral EFGH depend on its specific classification. However, some general properties of quadrilaterals include opposite sides being parallel, opposite angles being equal, and diagonals bisecting each other.
What are the applications of quadrilaterals?
Quadrilaterals are used in a wide variety of applications, including architecture, engineering, and design. For example, rectangles are used in the construction of buildings, trapezoids are used in the design of bridges, and kites are used in the construction of airplanes.