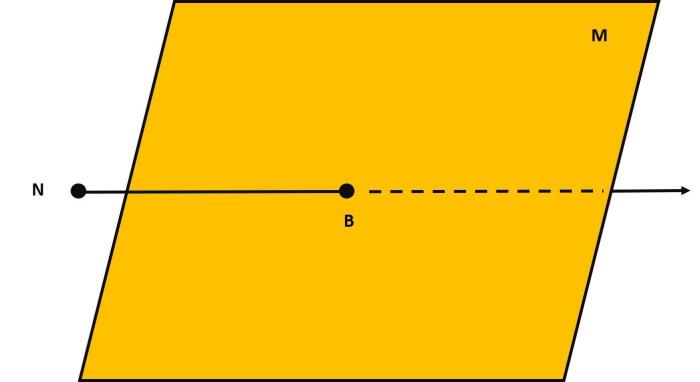
Plane M and NB intersecting at A introduces a captivating exploration into the intersection of two planes in three-dimensional space. This intersection point serves as a crucial concept with diverse applications across various fields, ranging from architecture to engineering and computer graphics.
Delving into the mathematical underpinnings, we will examine the equations representing planes and delve into the techniques used to determine their intersection point. Additionally, we will explore the angle formed between intersecting planes and uncover the practical implications of plane intersections in real-world scenarios.
Plane M and Plane N Intersection Overview

In three-dimensional space, planes are flat surfaces that extend infinitely. When two planes intersect, they form a line that lies on both planes.
The equation of a plane can be represented as Ax + By + Cz + D = 0, where A, B, C,and Dare constants and x, y,and zare the coordinates of a point on the plane.
For example, the plane with equation 2x- y + 3z – 5 = 0 contains all points (x, y, z)that satisfy this equation.
When two planes with equations A1x + B 1y + C 1z + D 1= 0 and A2x + B 2y + C 2z + D 2= 0 intersect, the line of intersection can be found by solving the system of equations.
Determining Intersection Point: Plane M And Nb Intersecting At A
To find the intersection point of two planes, we can use cross products and dot products.
The cross product of two vectors aand bis a vector ax bthat is perpendicular to both aand b.
The dot product of two vectors aand bis a scalar a· bthat is equal to the product of their magnitudes and the cosine of the angle between them.
To find the intersection point of two planes, we can first find two vectors that lie on the planes.
For example, if the planes have equations 2x- y + 3z – 5 = 0 and x + 2y- z + 1 = 0 , we can find two vectors that lie on the planes as follows:
- v1= (2, -1, 3)
- v2= (1, 2, -1)
The cross product of these two vectors is a vector that is perpendicular to both planes.
v1x v2= (-5, -5, 5)
This vector is parallel to the line of intersection of the two planes.
To find the intersection point, we can find a point that lies on both planes.
For example, the point (1, 1, 1)lies on both planes.
The intersection point is the point that lies on both planes and is parallel to the line of intersection.
To find the intersection point, we can use the following steps:
- Find two vectors that lie on the planes.
- Find the cross product of the two vectors.
- Find a point that lies on both planes.
- Find the intersection point by finding the point that lies on both planes and is parallel to the line of intersection.
Angle Between Intersecting Planes
The angle between two intersecting planes is the angle between their normal vectors.
The normal vector to a plane with equation Ax + By + Cz + D = 0is the vector n= ( A, B, C).
The angle between two vectors aand bis given by the following formula:
cos θ= ( a· b) / (|| a|| || b||)
where θis the angle between aand b, and || a|| and || b|| are the magnitudes of aand b, respectively.
To find the angle between two intersecting planes, we can use the following steps:
- Find the normal vectors to the planes.
- Find the dot product of the normal vectors.
- Find the magnitudes of the normal vectors.
- Use the formula above to find the angle between the planes.
Applications of Plane Intersections
Plane intersections have many applications in various fields, including:
- Architecture:Plane intersections are used to design buildings and other structures.
- Engineering:Plane intersections are used to design bridges, roads, and other infrastructure.
- Computer graphics:Plane intersections are used to create 3D models and animations.
For example, in architecture, plane intersections are used to create the plans and elevations of buildings.
In engineering, plane intersections are used to design the geometry of bridges and roads.
In computer graphics, plane intersections are used to create the 3D models of objects and environments.
Detailed FAQs
What is the significance of the intersection point of two planes?
The intersection point of two planes holds great importance as it represents the unique location in space where the two planes meet. This point serves as a reference for determining the angle between the planes and understanding their spatial relationship.
How can we calculate the angle between two intersecting planes?
The angle between two intersecting planes can be calculated using the dot product of their normal vectors. The dot product provides a measure of the cosine of the angle, which can then be converted to the angle itself using trigonometric functions.
What are some practical applications of plane intersections?
Plane intersections find applications in numerous fields, including architecture, engineering, and computer graphics. In architecture, they are used to determine the intersection of walls, roofs, and other structural elements. In engineering, they are employed in the design of bridges, tunnels, and aircraft.
In computer graphics, they are used to create realistic 3D models and scenes.